こんにちは、上位校突破塾ブルーの井上です。今回は多くの受験生が苦手意識を持ちがちな「確率」について面白い問題を紹介したいと思います。
確率の問題では、私たちの直感と数学的な計算結果が食い違うことがよくあります。こうした問題は入試でも頻出ですが、正しく理解していれば得点源になる分野です。今回は、特に勘違いしやすい確率問題を5つ紹介し、解説していきます。
1. 誕生日のパラドックス
問題:
一つの教室に何人集まれば、少なくとも2人の誕生日が同じになる確率が50%を超えるでしょうか?
よくある勘違い:
「365日÷2 = 183人程度」と考えてしまいがちです。
正しい考え方:
実は、わずか23人集まれば確率は50%を超えるのです!これを計算するコツは、「少なくとも2人の誕生日が同じ確率」を直接求めるのではなく、「全員の誕生日が異なる確率」を計算し、それを1から引くアプローチです。
具体的な計算は次のようになります:
- 1人目:365日/365 = 1 (どの日でもOK)
- 2人目:364日/365 (1人目と違う日)
- 3人目:363日/365 (先の2人と違う日)
- …
- 23人目:343日/365 (先の22人と違う日)
全員の誕生日が異なる確率 = 365/365 × 364/365 × 363/365 × … × 343/365 ≈ 0.493
したがって、少なくとも2人の誕生日が同じ確率 = 1 – 0.493 ≈ 0.507 (約50.7%)
こうした「直感と異なる結果」が出るのは、組み合わせの数が私たちの想像以上に急速に増えるためです。クラスの人数は大体30人くらいだと思うのでもしかしたらあなたのクラスの誰かと誰かは誕生日が同じかも。
2. モンティ・ホール問題
問題:
クイズ番組で、3つのドアがあります。1つのドアの後ろには車が、残りの2つのドアの後ろにはヤギがいます。あなたは1つのドアを選びました。司会者は残りの2つのドアのうち、ヤギがいるドアを1つ開けて見せました。ここであなたは、最初に選んだドアを変更すべきでしょうか?
よくある勘違い:
「残り2つのドアの確率は同じだから、変える必要はない」と考えがちです。
正しい考え方:
実は、最初の選択を変えることで当たる確率は”2倍”(1/3から2/3へ)になります!
これを理解するために、次のように考えましょう:
- 最初の選択で車を選ぶ確率は1/3
- 最初の選択でヤギを選ぶ確率は2/3
- 司会者はヤギのドアを開けるという情報を追加
- もし最初に「ヤギ」を選んでいた場合(確率2/3)、司会者が開けた後選んでいないもう一つのドアには必ず車がある
- したがって、「選択を変える」という戦略は2/3の確率で車が当たる。
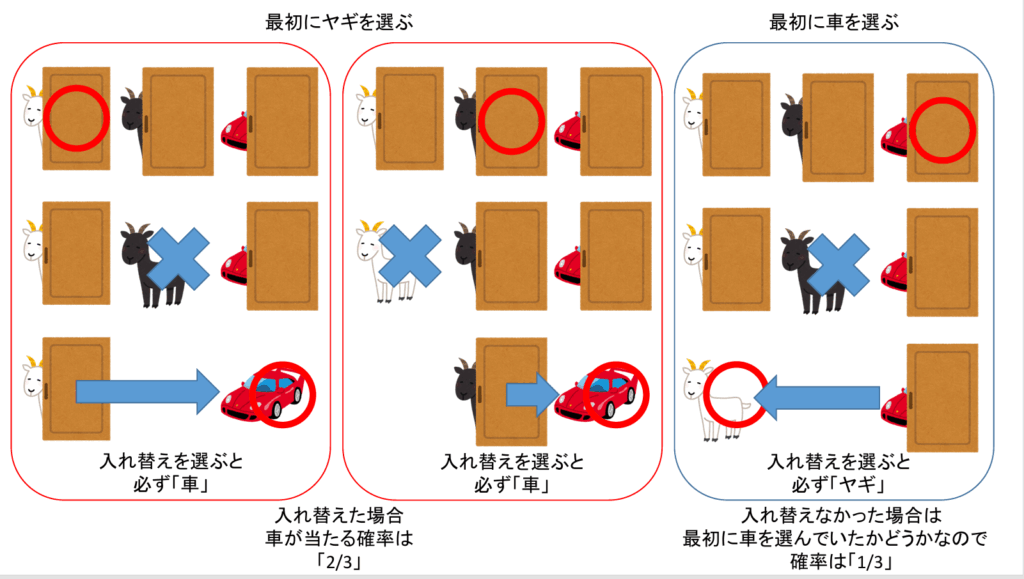
この問題は、「条件付き確率」の考え方を理解するのに非常に役立ちます。
3. 男女の産み分け問題
問題:
ある家族に2人の子どもがいます。そのうち少なくとも1人は男の子だとわかっています。この家族の子どもが2人とも男の子である確率はいくらですか?
よくある勘違い:
「男か女かの2通りだから1/2」と考えがちです。
正しい考え方:
実は、答えは1/3なのです。
可能性のある組み合わせは以下の4通りです:
- (男,男)
- (男,女)
- (女,男)
- (女,女)
このうち「少なくとも1人は男の子」という条件を満たすのは(女,女)以外の3通りです。その中で「2人とも男の子」なのは1通りなので、確率は1/3となります。
この問題では、条件を正確に捉えることが大切です。もし「長男が男の子」という条件だった場合、答えは1/2になります。
4. 同じ目が出る確率(サイコロ)
問題:
2つのサイコロを振って、同じ目が出る確率はいくらですか?
よくある勘違い:
「同じ目」を「特定の目(例:両方とも3)」と解釈してしまい、1/36と計算してしまいます。
正しい考え方:
「同じ目」とは(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)の6通りのことです。 可能な組み合わせ全体は6×6=36通りなので、確率は6/36=1/6となります。
この問題は解釈の仕方が重要です。問題文をしっかり読み、「何を求めているのか」を正確に把握することが必要です。
5. くじ引きの順序の影響
問題:
10本のくじがあり、そのうち3本が当たりです。2人が順番にくじを引く場合、最初の人と2番目の人が当たりくじを引く確率は同じでしょうか?
よくある勘違い:
「直感的には2番目の人は状況が変わるから確率も変わるはず」と考えがちです。
正しい考え方:
確かに状況は変わりますが、計算してみると両者の確率は同じになります。
最初の人が当たりを引く確率: 3/10 = 0.3
2番目の人が当たりを引く確率:
- 最初の人が外れを引いた場合(確率7/10): 当たりくじは3本のまま、残りは9本なので 3/9
- 最初の人が当たりを引いた場合(確率3/10): 当たりくじは2本になり、残りは9本なので 2/9
計算すると: (7/10)×(3/9) + (3/10)×(2/9) = 21/90 + 6/90 = 27/90 = 3/10 = 0.3
つまり、どちらも確率は0.3で同じです。これは「有限母集団からの非復元抽出(いわゆる中身に限りがあって引くとなくなっていくくじ)」における興味深い性質です。
この問題の教訓は「直感と異なる結果が出ることがあるため、確率はきちんと計算することが大切」ということになります。
まとめ:確率問題攻略のポイント
確率問題を解く際は、以下のポイントを意識しましょう:
- 条件をしっかり読み取る:問題文の条件を正確に把握することが第一歩
- 場合分けを丁寧に:起こりうる全ての場合を漏れなく数え上げる
- 直感に頼りすぎない:計算で確かめる習慣をつける
- 図や表を活用する:複雑な状況を整理するのに役立つ
- 条件付き確率の理解を深める:「〜という条件のもとでの確率」を正しく計算できるようにする
おわりに
確率の問題は、一見シンプルでも奥が深く、直感と計算結果が食い違うことがよくあります。しかし、それこそが確率の面白さでもあります。皆さんも、「なぜそうなるのか?」という疑問を大切に、確率の世界を楽しんでみてください。
入試では、このような「引っかかりやすい問題」がしばしば出題されます。日頃から直感に頼るだけでなく、しっかりと場合の数を数え上げる習慣をつけておくことが大切です。
上位校突破塾ブルーでは学習相談などの様々なご相談をお受けします!!
下のボタンからLINEを使用→トークでお気軽にご質問ください!!



コメント